树状数组(含Rotated Inversions题解)
本文背景
3.13 在解决 “F - Rotated Inversions”(逆序对问题)时,偶遇TLE强如怪物,拼尽归并排序无法战胜(实际上是我这蒟蒻写错了归并排序的位置导致的)。这道题折磨了我小半周,好在有传奇学长 Yffffff 热心相助。为铭记传奇学长,故写个Blog记录一下。
树状数组的概念及其构建
概念
树状数组是一种用于高效处理数组前缀和相关问题的数据结构。它能在对数时间内实现单点更新和区间查询操作,相比普通数组遍历求和,大大提高了效率,常用于解决数据统计、动态区间求和等问题。
构建过程
一. 最粗暴版(即依次两两求和)
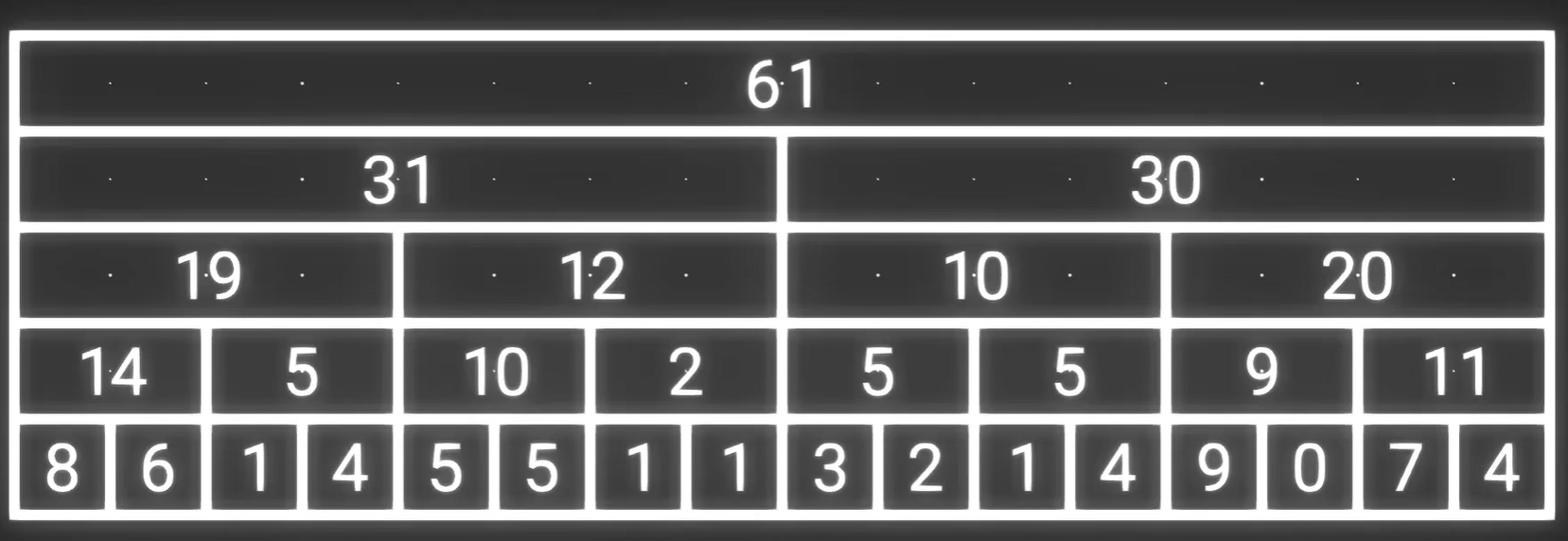
查询过程
eg:要计算前15个数字的和,只需要计算4个数字即可
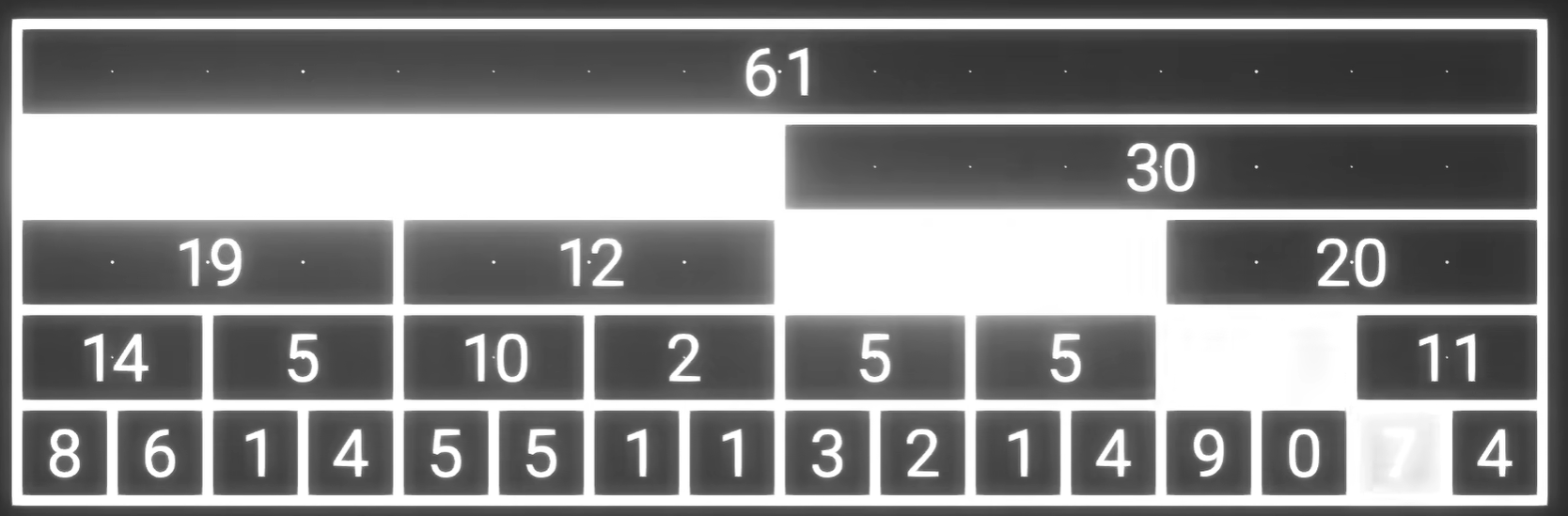
二. 离散化版
我们发现,表中的这些数字对于查询没有任何的帮助,去掉后如下。

剩下的数据按照出现顺序写成一排如下:

不难发现:这个数组和原始数据正好一样长!
我们就构建了一个离散化的树状数组,而树状数组中的每一个元素,刚好对应下面每一个区间。
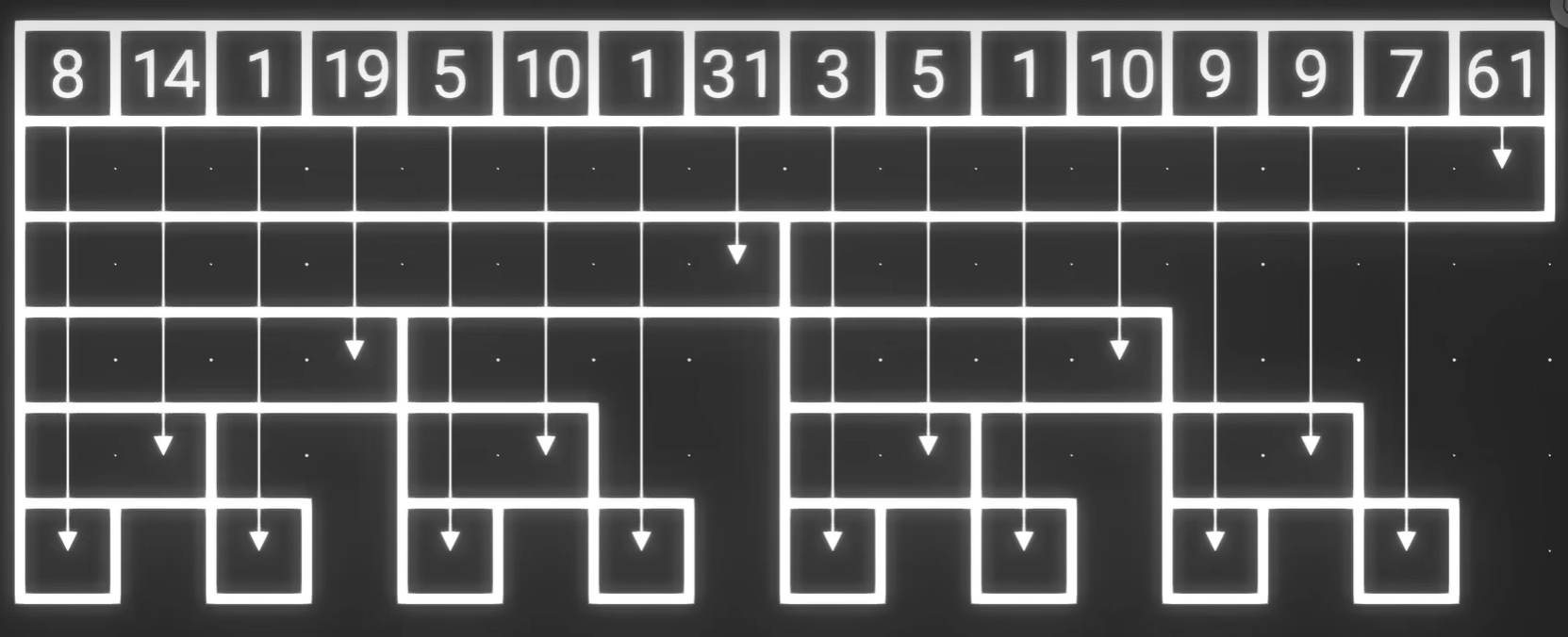
对于查询: 我们从要查找的元素位置依次向左向上推,相加即是答案。
对于修改: 我们从要查找的元素位置依次向右向上推,每个数都相加上修改的值。
三. 视频
代码核心:lowbit()函数介绍
这个函数会求出一个二进制数字的最低位代表哪个数字
代码如下:
1
2
3
4
|
int lowbit(int x)
{
return x & -x;
}
|
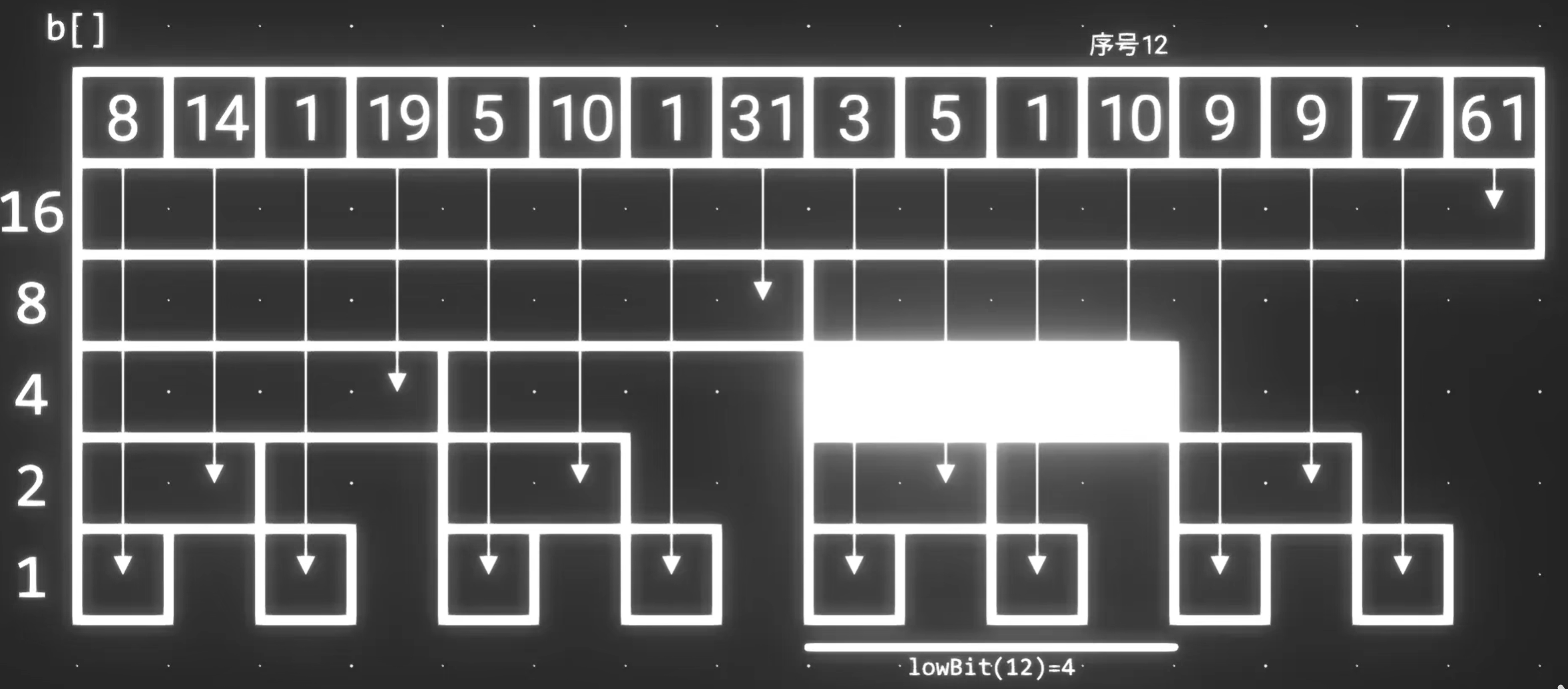
而对于离散化的树状数组,我们发现:
1. 其中第k个元素对应的下标的lowbit刚好等于其所对应的原数组中的元素长度
2. 其中第k个元素对应正上方的序列的元素下标正好就是lowbit(k)+k
因此,查询时,只需要不断的循环加上b[k]+b[k-lowbit(k)]直到开头为止,进行相加;修改时,只需要不断加上lowbit(k)就可以找到上方的所有序列,进行修改。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
int lowbit(int x)
{
return x & -x;
}
void add(int pos,int x)
{
while(pos<=n)
{
tree[pos]+=x;
pos+=lowbit(pos);
}
}
int sum(int pos)
{
int ans = 0;
while(pos)
{
ans+=tree[pos];
pos-=lowbit(pos);
}
return ans;
}
|
树状数组在求逆序对问题上的应用
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
struct node{
int val,pos;
bool operator<(const node x)
{
if(val==x.val) return pos>x.pos;//值一样,位置大的现在前面
return val > x.val;//不然值大的在前面
}
};
int a[N];
vector<node> vt;
vector<int> arr[N];
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
vt.push_back({a[i],i});
arr[a[i]].push_back(i);
}
sort(vt.begin(),vt.end());
for(auto k:vt)
{
int pos=k.pos;
res+=sum(pos-1);
add(pos,1);
}
cout << res << endl;
}
|
归并排序实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
#include "bits/stdc++.h"
#define int long long
using namespace std;
const int N = 2e6 + 10; //100005
int n,m;
int a[N];
int b[N];
vector<int> arr[N];
int mergesort(int l,int r)
{
if(l>=r) return 0;
int mid = (l+r) >> 1;
int res = mergesort(l,mid) + mergesort(mid+1,r);
int i = l,j = mid+1,k = l;
while(i<=mid&&j<=r)
{
if(a[i]<=a[j])
b[k++] = a[i++];
else
{
b[k++] = a[j++];
res += mid - i + 1;
//如果发生从j后面中拿元素,说明a中i位置全比该元素大
//所以构成了mid-i+1个逆序对
}
}
while(i<=mid) b[k++] = a[i++];
while(j<=r) b[k++] = a[j++];
for(int i=l;i<=r;i++) a[i] = b[i];
return res;
}
void solve()
{
cin >> n >> m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
arr[a[i]].push_back(i);
}
int res = mergesort(1,n);
cout << res << endl;
for(int k=1;k<=m-1;k++)
{
for(int j=0;j<(int)arr[m-k].size();j++)
{
res+=arr[m-k][j]-1-j;
res-=(n-arr[m-k][j]-(arr[m-k].size()-j-1));
}
cout<<res<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int _ = 1;
// cin >> _ ;
while(_--)
{
solve();
}
return 0;
}
|
树状数组实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
|
#include "bits/stdc++.h"
#define int long long
using namespace std;
const int N = 2e6 + 10; //100005
struct node{
int val,pos;
bool operator<(const node x)
{
if(val==x.val) return pos>x.pos;
return val > x.val;
}
};
int n,m,res;
int a[N],tree[N];
vector<int> arr[N];
vector<node> vt;
int lowbit(int x)
{
return x & -x;
}
void add(int pos,int x)
{
while(pos<=n)
{
tree[pos]+=x;
pos+=lowbit(pos);
}
}
int sum(int pos)
{
int ans = 0;
while(pos)
{
ans+=tree[pos];
pos-=lowbit(pos);
}
return ans;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
vt.push_back({a[i],i});
arr[a[i]].push_back(i);
}
sort(vt.begin(),vt.end());
for(auto k:vt)
{
int pos=k.pos;
res+=sum(pos-1);
add(pos,1);
}
cout << res << endl;
for(int k=1;k<=m-1;k++)
{
for(int j=0;j<(int)arr[m-k].size();j++)
{
res+=arr[m-k][j]-1-j;
res-=(n-arr[m-k][j]-(arr[m-k].size()-j-1));
}
cout<<res<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int _ = 1;
// cin >> _ ;
while(_--)
{
solve();
}
return 0;
}
|
两段代码关键点解释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
for(int k=1;k<=m-1;k++)
//遍历 k 从 1 到 (M - 1)的所有可能取值。对于每个 k 值,都要计算对应序列 B 的逆序对数量
{
for(int j=0;j<(int)arr[m-k].size();j++)
//当 k 增加 1 时,原序列中值为 (m - k) 的元素,在新的 B 序列里会变成值为 0 的元素,因为 (m - k + 1) mod M = 0
//意思是把这次加上k等于M的数全部找出来,因为M mod M = 0,意味着此时这个数小于序列中的任何数,与他前面的数新构成了逆序对
{
res+=arr[m-k][j]-1-j;
//arr[m - k][j] - 1 表示该元素前面一共有多少个元素
//j 表示在 arr[m - k] 这个数组里,该元素前面值同样为 (m - k) 的元素个数
//所以 arr[m - k][j] - 1 - j 就代表该元素前面值小于 (m - k) 的元素数量
//当 k 增加 1 后,这个元素的值变为 0,它会和前面那些不等于这个数且值小于 (m - k) 的元素构成新的逆序对
//所以对前面的数(排除和这个数相等的),要加上这个数的贡献
res-=(n-arr[m-k][j]-(arr[m-k].size()-j-1));
//n - arr[m - k][j] 表示该元素后面元素的总数
//arr[m - k].size() - j - 1 表示在 arr[m - k] 里,该元素后面值同样为 (m - k) 的元素个数
//所以 n - arr[m - k][j] - (arr[m - k].size() - j - 1) 就代表该元素后面值大于 (m - k) 的元素数量
//当 k 增加 1 后,这个元素的值变为 0,它和后面那些不等于这个数且值大于 (m - k) 的元素就不再构成逆序对了
//所以要从 res 里减去他的贡献
}
cout<<res<<endl;
}
|





