线段树

线段树：线段树是一种二叉树数据结构。其每个节点代表一个区间，根节点代表整个区间，叶子节点代表最小子区间，是平衡二叉树，高度为$(O(log n))$。它能高效进行区间查询、单点修改和区间修改等操作，操作时间复杂度一般为$ (O(log n))$，常用于数组统计、区间更新与查询等场景，可提高相关算法的时间和空间复杂度。

建树（分治思想）

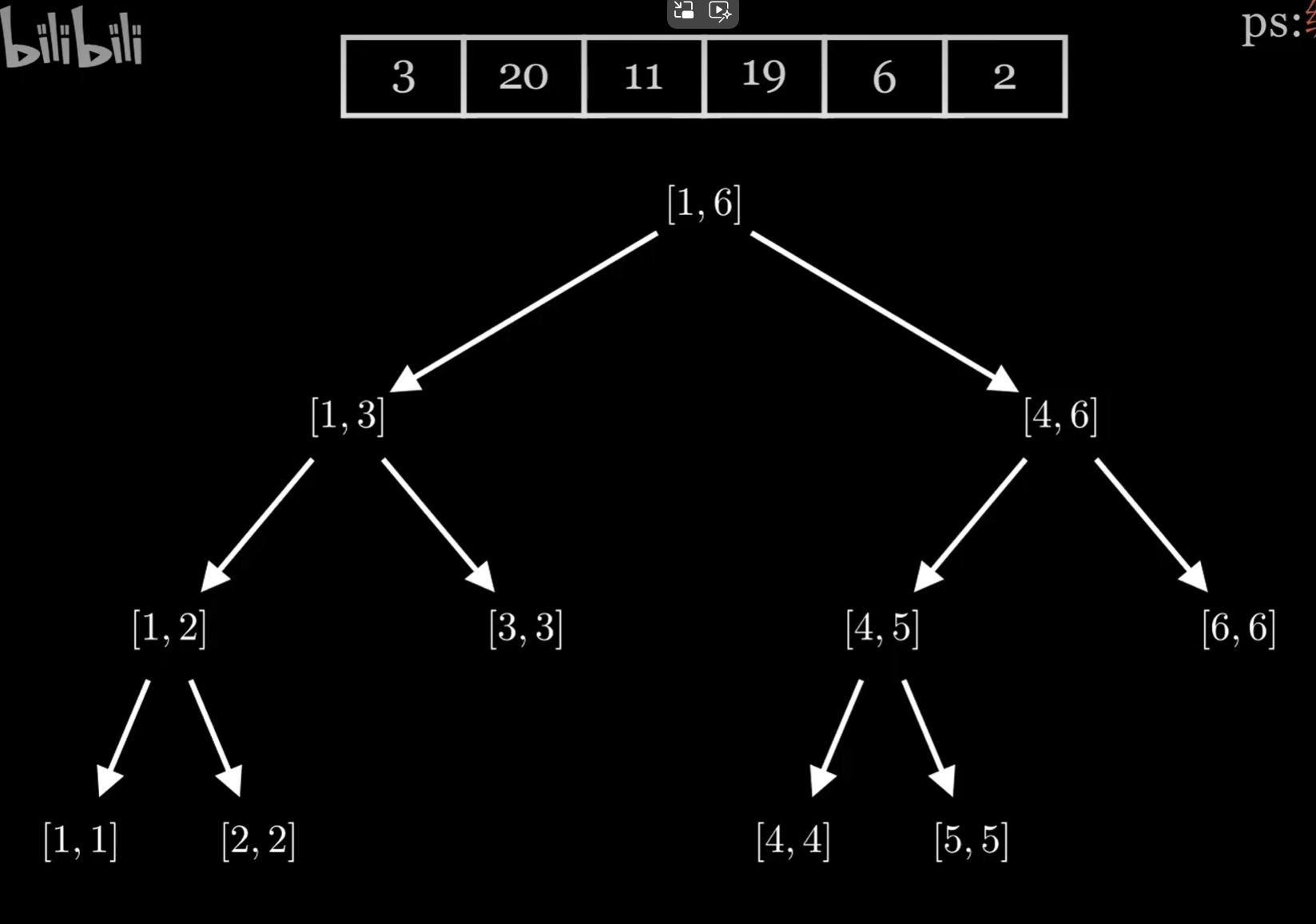
通过观察，发现我们如果为每个节点补足NULL，它形成了一个完全二叉树，于是我们有以下的规律：

$$ parent_i = \left\lfloor \frac{i}{2} \right\rfloor $$$$ left_i = 2 * i , right_i = 2 * i + 1 $$

每个节点存储下各自对应区间的最大值，于是我们得到：

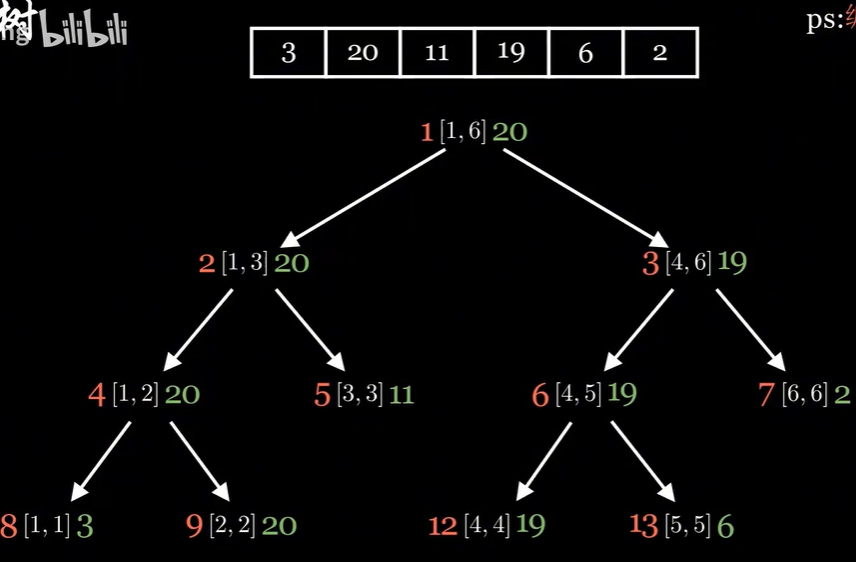
区间查询

假设我们要查找区间$ [2,3] $的最大值，我们先看到root节点，发现$[2,3]$与$[1,6]$并不完全匹配，所以我们继续向下遍历，当到达节点4的时候，发现$[2,3]$与其左右孩子均有交集，于是我们兵分两路，分别以此类推的去找$[2,2]$和$[3,3]$的最大值。

最后找到5和9节点，答案就为$max(tree[5],tree[9])$

单点更新

假设我们尝试把原数组的第二个数字更新为6，我们一样按照区间查询的思想找到$[2,2]$这个节点，并依次向上更新整个线段树。

区间更新

定义：为一个区间内的所有值加上一个常数。

为了使得时间复杂度保持在$O(logn)$，于是我们引入一个新的概念——懒标记，由于最初没有任何区间更新，于是我们初始化所有懒标记为0。

我们尝试令区间$[4,6]$的每个元素+1，还是按照区间查询的思想找到符合的节点，这里我们找到节点3，发现它与我们要更新的节点完全匹配，于是我们把节点3的值加上1，为了优化性能，我们在这里偷个懒——把更新请求存储到节点3的lazy标记上，如下图所示：

所以懒标记的作用就是允许我们延迟更新操作，只在有需求的时才真正执行。

最后别忘了依次向上更新数组。

我们再来假设给$[4,5]$的每个元素+1，依旧先找到匹配的节点。

当到达节点3的时候，我们发现区间并不完全匹配，于是在继续向下更新时，我们要先检查节点3的lazy标记，由于其不为0，说明之前有偷懒未执行的更新操作，所以此时要对lazy标记进行“下发”处理：将其标记的值1传递给其左右孩子节点6和7，更新6,7的值和懒标记，同时归零节点3的懒标记，如下图所示：

接着遍历，我们来到节点6，发现此时节点6与查询区间$[4,5]$完全匹配，于是我们更新节点6的值，并且在节点6的懒标记上加上我们的更新请求，如图所示：

最后还是别忘了依次向上更新数组。

懒标记对区间查询和单点更新的影响

由于懒标记的特性，所以在进行区间查询或单点更新的时候，如果遇到某个节点有懒标记，我们必须先对lazy标记进行“下发”处理，然后再继续查询。

当然，单点更新还是别忘了依次向上更新数组。

代码实现

我们先定义一个node节点：

1
2
3


struct node {
    int data, lazy = 0;
};

接下来我们实现了线段树的构建函数build：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


void build(const vector<int> &data, vector<node> &tree, int rt, int left, int right) {
    if (left == right) {
        tree[rt].data = data[left];//叶子节点
        return;
    }
    int mid = left + (right - left) / 2;
    build(data, tree, 2*rt, left, mid);//递归构建左子树
    build(data, tree, 2*rt + 1, mid + 1, right);//递归构建右子树
    tree[rt].data = max(tree[2 * rt].data, tree[2 * rt + 1].data);//更新当前节点的值
}

对于懒标记的处理pushDown：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void pushDown(vector<node> &tree, int rt) {
    if(tree[rt].lazy != 0) {
        //更新左子树
        tree[2 * rt].data += tree[rt].lazy;
        tree[2 * rt].lazy += tree[rt].lazy;
        //更新右子树
        tree[2 * rt + 1].data += tree[rt].lazy;
        tree[2 * rt + 1].lazy += tree[rt].lazy;
        //清空当前节点的懒标记
        tree[rt].lazy = 0;
    }
}

查询函数query:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


int query(vector<node> &tree, int rt, int left,int right,int ql,int qr) {
    if (ql > right || qr < left) {
        return INT_MIN; // 若区间无交集，返回最小值，表明该区间对结果无贡献
    }
    if (ql <= left && qr >= right) {
        return tree[rt].data; // 若完全包含，直接返回当前节点的值
    }
    int mid = left + (right - left) / 2;
    pushDown(tree, rt); // 若当前节点有延迟标记，将其下推到子节点
    int leftMax = query(tree, 2*rt, left, mid, ql, qr); // 递归查询左子树
    int rightMax = query(tree, 2*rt+1, mid+1, right, ql, qr); // 递归查询右子树
    return max(leftMax, rightMax);
}

单点更新函数update：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


void update(vector<node> &tree, int rt, int left, int right, int idx, int value) {
    if(left == right){
        tree[rt].data = value;
        tree[rt].lazy = 0;//找到目标节点，更新值
        return;
    }
    int mid = left + (right - left) / 2;
    pushDown(tree, rt);//处理懒标记
    if(idx <= mid) update(tree, 2*rt, left, mid, idx, value);
    else update(tree, 2*rt+1, mid+1, right, idx, value);
    tree[rt].data = max(tree[rt*2].data, tree[rt*2+1].data);
}

区间更新函数updateRange：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


void updateRange(vector<node> &tree, int rt, int left, int right, int ul, int ur, int value){
    if(ul > right || ur < left) return; //区间无交集，直接返回
    if(ul <= left && ur>= right) {
        tree[rt].data += value; //更新当前节点的值
        tree[rt].lazy += value; //设置懒标记
        return;
    }
    int mid = left + (right - left) / 2;
    pushDown(tree, rt); //处理懒标记
    updateRange(tree, 2*rt, left, mid, ul, ur, value); //更新左子树
    updateRange(tree, 2*rt+1, mid+1, right, ul, ur, value); //更新右子树
    tree[rt].data = max(tree[rt*2].data, tree[rt*2+1].data); //更新当前节点的值
}

最后强调：为了避免越界问题，线段树的大小通常会初始化为原始区间大小的4倍

class模板

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84


struct node {
	int data, lazy = 0;
};

class SegTree {
public:
	int n, root, L, R;
	vector<int> data;
	vector<node> tree;
	
	SegTree(int _n, int _rt, int _L, int _R)
	: n(_n), root(_rt), L(_L), R(_R), data(n+1), tree(4*n) {}
	
	// 对外接口
	void build() { build(root, L, R); }
	void update(int idx, int value) { update(root, L, R, idx, value); }
	void updateRange(int ul, int ur, int value) { updateRange(root, L, R, ul, ur, value); }
	int query(int ql, int qr) { return query(root, L, R, ql, qr); }
	
private:
	void build(int rt, int left, int right) 
	{
		if (left == right) {
			tree[rt].data = data[left];//叶子节点
			return;
		}
		int mid = left + (right - left) / 2;
		build(2*rt, left, mid);//递归构建左子树
		build(2*rt + 1, mid + 1, right);//递归构建右子树
		tree[rt].data = max(tree[2 * rt].data, tree[2 * rt + 1].data);//更新当前节点的值
	}
	void pushDown(int rt) 
	{
		if(tree[rt].lazy != 0) {
			//更新左子树
			tree[2 * rt].data += tree[rt].lazy;
			tree[2 * rt].lazy += tree[rt].lazy;
			//更新右子树
			tree[2 * rt + 1].data += tree[rt].lazy;
			tree[2 * rt + 1].lazy += tree[rt].lazy;
			//清空当前节点的懒标记
			tree[rt].lazy = 0;
		}
	}
	int query(int rt,int left,int right,int ql,int qr) {
		if (ql > right || qr < left) {
			return INT_MIN; // 若区间无交集，返回最小值，表明该区间对结果无贡献
		}
		if (ql <= left && qr >= right) {
			return tree[rt].data; // 若完全包含，直接返回当前节点的值
		}
		int mid = left + (right - left) / 2;
		pushDown(rt); // 若当前节点有延迟标记，将其下推到子节点
		int leftMax = query(2*rt, left, mid, ql, qr); // 递归查询左子树
		int rightMax = query(2*rt+1, mid+1, right, ql, qr); // 递归查询右子树
		return max(leftMax, rightMax);
	}
	void update(int rt, int left, int right, int idx, int value) 
	{
		if(left == right){
			tree[rt].data = value;
			tree[rt].lazy = 0;//找到目标节点，更新值
			return;
		}
		int mid = left + (right - left) / 2;
		pushDown(rt);//处理懒标记
		if(idx <= mid) update(2*rt, left, mid, idx, value);
		else update(2*rt+1, mid+1, right, idx, value);
		tree[rt].data = max(tree[rt*2].data, tree[rt*2+1].data);
	}
	void updateRange(int rt, int left, int right, int ul, int ur, int value){
		if(ul > right || ur < left) return; //区间无交集，直接返回
		if(ul <= left && ur>= right) {
			tree[rt].data += value; //更新当前节点的值
			tree[rt].lazy += value; //设置懒标记
			return;
		}
		int mid = left + (right - left) / 2;
		pushDown(rt); //处理懒标记
		updateRange(2*rt, left, mid, ul, ur, value); //更新左子树
		updateRange(2*rt+1, mid+1, right, ul, ur, value); //更新右子树
		tree[rt].data = max(tree[rt*2].data, tree[rt*2+1].data); //更新当前节点的值
	}
};