图的存储:链式前向星
本文背景
在解决倍增算法时发现该算法主要用于解决LCA(最近公共祖先)问题,于是转来看了看,看到了一种新的图存储方式(布什戈门,你还有啊!!),于是来写写这个B新存储方式:链式前向星。
头插存储法(链式前向星)
概念
链式前向星结合了链表和数组的特点,其核心思想是通过数组模拟链表来存储图的边信息。它用一个数组 head 来记录每个顶点的第一条边的编号,同时用一个结构体数组 edge 来存储每条边的具体信息,包括边的终点和下一条边的编号。
edge数组
对于一个图:
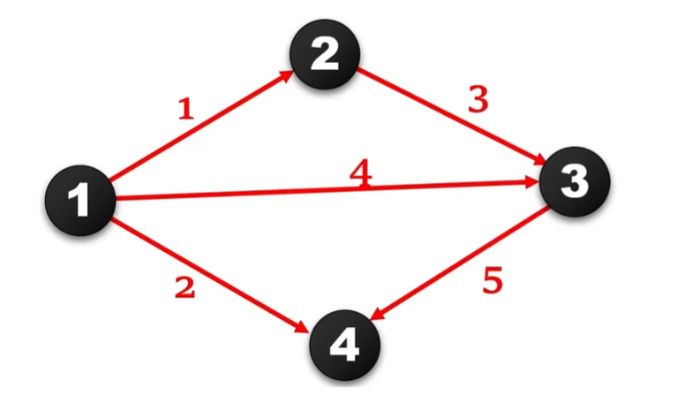
我们看到1到2的这条边,发现边的信息有:起点(from),权值(wealth),终点(to),于是我们有结构体如下:
1
2
3
4
|
struct node
{
int fr,w,to;
};
|
这是最直观的想法,但是我们发现如果真的这样存储的话,所有的信息会非常散乱,即一个点的边的信息的存储完全由输入的顺序决定,最坏情况可能就是有两个信息在输入开头和结尾,这显然会对遍历带来麻烦,于是我们引入了head数组。
head数组
如果我们想把一个点的所有边的数据整合一下的话,从物理层面上来说是把这些数据放到一起,但是对于内存这种奇葩的东西(整理过的都知道好)我们还是用一个结构分别记录每个点在edge数组中的位置吧。
但聪明的你很快又发现:这不又是一个图了吗?(bushi),但很快你就发现,我们可以用链表(和C语言课上学的那种不完全一样)来打败这么多个图,即$ head[x] $表示输入流中$x$节点的最后一条边所在edge数组中的位置。
这时候就有观众要问了:煮波煮波,head数组固然很强,那我们有没有找到输入流中$x$节点的非最后一条边所在edge数组中的位置的方法呢?
有的兄弟,有的。
我们只需要在node中加入一个新的量nxt去指向上一个节点的位置(链表bushi),而$ from $ 这个数据则体现在了head的下标中。
综上所述,我们对node的定义如下:
1
2
3
4
|
struct node
{
int to,w,nxt;
};
|
对这个例子,我们可以形象化的看到我们的数据结构如下:
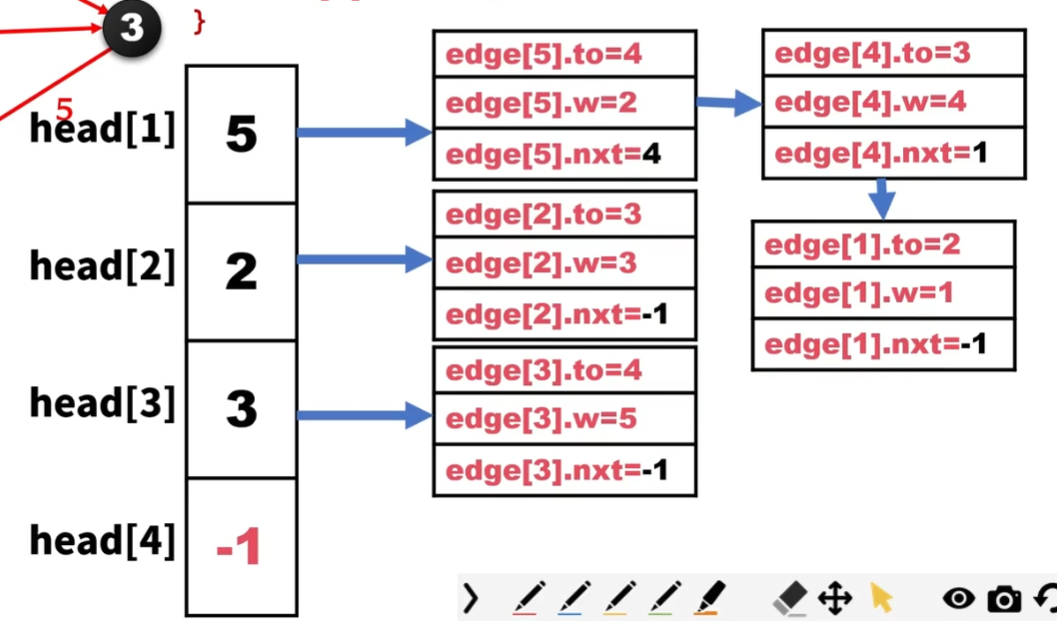
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
struct node
{
int nxt,w,to;
};
int head[N];
node edge[N];
int cnt;
void add_edge(int from,int w,int to)
{
//这里以双向图为例
//先更新cnt是因为不想出现0这个点
edge[++cnt].nxt = head[from];
//指向from这个点的上一次输入进来边的信息的位置(edge)
edge[cnt].to = to;
edge[cnt].w = w;
//from指向的点to和边权
head[from] = cnt;
//更新head中from这个点的记录的最后一个点(edge)的信息
//反向边同理
edge[++cnt].nxt = head[to];
edge[cnt].to = from;
edge[cnt].w = w;
head[to] = cnt;
}
|
视频讲解
前置知识点
倍增算法(含L3-1 银白之森题解)
思路
我们现尽可能让深度更深的节点(设为$x$)尽量的大的跳,不断减少跳的次数,直到跳不下去为止,然后我们来看$x$和$y$是否跳到了同一个节点,是,找到了LCA,直接返回;否就$x$和$y$一起接着跳,直到找到LCA为止。
代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
#include "bits/stdc++.h"
#define int long long
using namespace std;
const int N = 1e6 + 10; //100005
struct node
{
int nxt,to;
};
int head[N],dep[N],f[N][25];
node edge[N];
int n,m,s;
int cnt;
void add_edge(int from,int to)
{
//双向图
edge[++cnt].nxt = head[from];
edge[cnt].to = to;
head[from] = cnt;
edge[++cnt].nxt = head[to];
edge[cnt].to = from;
head[to] = cnt;
}
void dfs(int v,int fa)
{
dep[v]=dep[fa]+1;
//更新该点的深度
for(int i=1;(1<<i)<=dep[v];i++)
f[v][i] = f[f[v][i-1]][i-1];
//预处理这个点跳2^i次方到的点
for(int i=head[v];i;i=edge[i].nxt)
{
//递归dfs
int p = edge[i].to;
if(p!=fa)
{
f[p][0] = v;
dfs(p,v);
}
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
//这一步是为了处理深的那个点
for(int i=20;i>=0;i--)
//找这个点跳2^i次方到的点(假设最大是2^20)
{
if(dep[f[x][i]]>=dep[y]) x=f[x][i];
//意思是先跳到最远,然后有近的就退
if(x==y) return x;
//是,那么return
}
//否就x和y一起接着跳,直到跳到了x,y不是一个祖先了
for(int i=20;i>=0;i--)
{
if(f[x][i]!=f[y][i])
{
x = f[x][i];
y = f[y][i];
}
}
//那么x或y任意一个往上走2^0(即1)就到了LCA
return f[x][0];
}
void solve()
{
cin >> n >> m >> s;
for(int i=1;i<=n-1;i++)
{
int x,y;
cin >> x >> y;
add_edge(x,y);
}
dfs(s,0);
for(int i=1;i<=m;i++)
{
int a,b;cin >> a >> b;
cout << lca(a,b) << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int _ = 1;
// cin >> _ ;
while(_--)
{
solve();
}
return 0;
}
|


