并查集及其进阶
普通并查集
并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
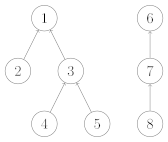
两种操作:
- 合并(Union):合并两个元素所属集合(合并对应的树)
- 查询(Find):查询某个元素所属集合(查询对应的树的根节点),这可以用于判断两个元素是否属于同一集合
并查集在经过修改后可以支持单个元素的删除、移动;使用动态开点线段树还可以实现可持久化并查集。
初始化
初始时,每个元素都位于一个单独的集合,表示为一棵只有根节点的树。方便起见,我们将根节点的父亲设为自己。
1
|
for(int i=1;i<=n;i++) fa[i] = i;
|
查询
我们需要沿着树向上移动,直至找到根节点。
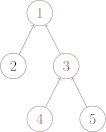
1
2
3
4
5
|
int find(int x)
{
if(x!=fa[x]) return find(fa[x]);
return fa[x];
}
|
路径压缩
查询过程中经过的每个元素都属于该集合,我们可以将其直接连到根节点以加快后续查询。
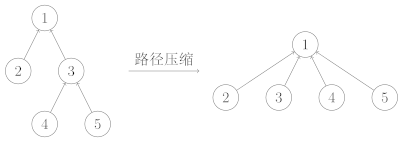
1
2
3
4
5
|
int find(int x)
{
if(x!=fa[x]) return fa[x] = find(fa[x]);
return fa[x];
}
|
合并
要合并两棵树,我们只需要将一棵树的根节点连到另一棵树的根节点。
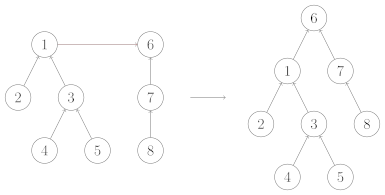
1
2
3
4
5
6
7
8
9
10
|
bool merge(int x,int y)
{
int fx = find(x),fy = find(y);
if(fx!=fy)
{
fa[fx] = fy;
return true;
}
return false;
}
|
删除
要删除一个叶子节点,我们可以将其父亲设为自己。为了保证要删除的元素都是叶子,我们可以预先为每个节点制作副本,并将其副本作为父亲。
移动
与删除类似,通过以副本作为父亲,保证要移动的元素都是叶子。
复杂度
时间复杂度
同时使用路径压缩和启发式合并之后,并查集的每个操作平均时间仅为 $O(\alpha(n))$,其中 $\alpha$ 为阿克曼函数的反函数,其增长极其缓慢,也就是说其单次操作的平均运行时间可以认为是一个很小的常数。
Ackermann函数: $A(m, n)$ 的定义是这样的:
$$
A(m, n) = \begin{cases}n+1&\text{if }m=0\\A(m-1,1)&\text{if }m>0\text{ and }n=0\\A(m-1,A(m,n-1))&\text{otherwise}\end{cases}
$$而反 Ackermann 函数 $\alpha(n)$ 的定义是阿克曼函数的反函数,即为最大的整数 $m$ 使得 $A(m, m) \leqslant n$。
空间复杂度
显然为 $O(n)$。
例题
P1536 村村通
STD:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
const int N = 1010; //100005
int f[N];
int find(int x)
{
if(x != f[x]) f[x] = find(f[x]);
return f[x];
}
void ship(int a,int b)
{
int fa = find(a),fb = find(b);
if(fa != fb) f[fa] = fb;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int n,m;
while(1)
{
cin >> n;
if(!n) break;
cin >> m;
for(int i=1;i<=n;i++) f[i] = i;
while(m--)
{
int a,b;
cin >> a >> b;
ship(a,b);
}
int ans = 0;
for(int i=1;i<=n;i++)
if(f[i]==i) ans++;
cout << ans - 1 << endl;
}
return 0;
}
|
带权并查集
我们还可以在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算,从而解决更多的问题。
相对祖先的距离
通过在节点之间记录距离值$dist[x]$,表示节点 x 到其父节点之间的“差值”。在路径压缩时递归累加这些差值,从而使 find 操作返回节点与根之间的累积差距。
find函数新的实现
1
2
3
4
5
6
7
8
9
10
|
int find(int x)
{
if(fa[x]!=x)
{
int t = fa[x];
dis[x] += dis[fa[x]];
fa[x] = t;
}
return fa[x];
}
|
例题
「NOI2002」银河英雄传说
思路
对于每个点,分别记录所属链的头结点、该点到头结点的距离以及它所在集合的大小。
每次合并将$y$接在$x$的尾部,改变y头的权值和所属链的头结点,同时改变$x$的尾节点。
注意:每次查找的时候也要维护每个节点的权值。
每次查询时计算两点的权值差。
STD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
const int N = 5e4+10; //100005
int f[N],front[N],num[N];
int find(int x)
{
if(f[x]!=x)
{
int t = find(f[x]);
front[x] += front[f[x]];
f[x] = t;
}
return f[x];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int t,x,y;
char op;
for(int i=1;i<=30000;i++) f[i] = i,num[i]=1;
cin >> t;
while(t--)
{
cin >> op >> x >> y;
int fx = find(x),fy = find(y);
if(op=='M')
{
front[fx] += num[fy];
num[fy] += num[fx];
num[fx] = 0;
f[fx] = fy;
}
else
{
if(fx != fy) cout << -1 << endl;
else cout << abs(front[x]-front[y]) - 1 << endl;
}
}
return 0;
}
|
扩展域并查集
扩展域并查集是在经典并查集中,增加多个“关系域”的支持(例如“吃、被吃”的关系),通过对元素映射成多个身份来维护复杂关系。
域的扩展
通常使用 $kn$ 大小的结构,为每个原始元素构造$k$个代表身份,再根据操作进行合并判断。
例题
「NOI2001」食物链
思路
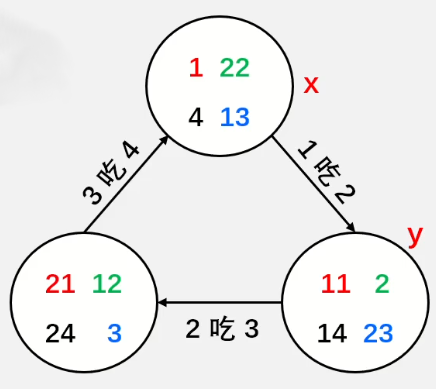
建立三倍节点标号:每个动物 $i$ 映射为$i$、$i+n$、$i+2n$ 分别代表自身、捕食者、天敌;根据陈述操作进行合并并判断是否矛盾。
注意:这里认为能量能循环流动(不符合生物学),不然无法得出推论三。
给 $x$ 在其他集合内安插两个“虚拟代表”,从而实现关系传递。
-
推论一:$x$ 吃 $y$,则 x 与 y 的天敌代表 $y + 2n$ 是同类,合并$(x, y + 2n)$;
-
推论二:$x$ 吃 $y$,则 x 的捕食代表 $x + n$ 与 y 是同类,合并 $(x + n, y)$;
-
推论三:$x$ 吃 $y$,则 x 的天敌代表 $x + 2n$ 与 y 的捕食代表 $y + n$ 是同类,合并 $(x + 2n, y + n)$。
STD
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
//#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define endl "\n"
#define int long long
using namespace std;
const int N = 1e6+10;
const int inf = 1e18+10;
int fa[N];
int ans;
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void solve()
{
int n,k;cin >> n >> k;
for(int i=1;i<=3*n;i++) fa[i] = i;
auto merge = [](int x,int y)
{
fa[find(y)] = find(x);
};
for(int i=1;i<=k;i++)
{
int op,x,y;cin >> op >> x >> y;
if(x>n or y>n) ans++;
else if(op==1)
{
if(find(x)==find(y+n) or find(x)==find(y+n+n)) ans++;
else
{
merge(x,y);
merge(x+n,y+n);
merge(x+n+n,y+n+n);
}
}
else
{
if(find(x)==find(y) or find(x)==find(y+n)) ans++;
else
{
merge(x,y+n+n);
merge(x+n,y);
merge(x+n+n,y+n);
}
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
int _ = 1;
//cin >> _;
while(_--)
{
solve();
}
return 0;
}
|
本题也可以通过带权并查集实现
习题
「NOI2015」程序自动分析
「JSOI2008」星球大战
1850H - Codeforces





